[toc]
软件设计师笔记03_数据结构_精简考点
科目一考试中占5分左右。
线性表
线性表常采用顺序存储和链式存储,主要的基本操作是插入、删除和查找等。
- 给定一个有n个元素的有序线性表。若采用顺序存储结构,则在等概率前提下,删除其中的一个元素平均需要移动 (n-1)/2 个元素。
- 当线性表进行顺序存储时,逻辑上相邻的元素,其物理位置也相邻。此时查询元素的时间复杂度为O(1),也就是常量级。此时插入元素就需要移动一些元素了,因此插入元素的时间复杂度为O(n),其中n为线性表的长度。
- 当线性表进行链式存储时,逻辑上相邻的元素,其物理位置不要求相邻。此时查找元素和插入元素的时间复杂度都为O(n)。
单向循环链表由于指针方向是单向的。因此访问其直接后继的运算时间复杂度为O(1),访问其直接前驱的运算时间复杂度为O(n)。
栈
- 栈是一种按“后进先出”原则进行插入和删除操作的数据结构,因此 实现函数或过程的递归调用及返回处理时 必须用栈。
- 表达式采用逆波兰式(后缀式)表示时,利用( 栈 )进行求值。
存放操作数的栈的容量
如何计算存放操作数的栈的至少容量:
- 先将表达式转换为后缀式。
- 然后看后缀式中的第一个运算符号前的操作数个数。那就是存放操作数的栈的至少容量。
例题
当利用栈对算术表达式10*(40-30/5)+20求值时,存放操作数的栈(初始为空)的容星至少为__,才能满足暂存该表达式中的运算数或运算结果的要求。
解法
- 先将表达式转换为后缀式 10 40 30 5 / - * 20 +
- 然后看后缀式中的第一个运算符号前的操作数个数。那就是存放操作数的栈的容量。
- 后缀式 10 40 30 5 / - * 20 + 中第一个运算符号前的操作数个数是4个。
则存放该操作树的栈的容量为4
队列
- 循环队列中求队头元素的指针的计算公式为:(rear-len+1+M) % M 其中rear是队尾指针,len是队列长度,M是队列存储容量。
- 必须采用队列结构的是 打印序列。
真题案例1
输出受限的双端队列是指元素可以从队列的两端输入,但只能从队列的一端输出,如下图所示,若有e1,e2,e3,e4依次进入输出受限的双端队列,则得不到输出序列 ( )。
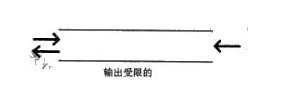
- A e4,e3,e2,e1
- B e4,e2,e1,e3
- C e4,e3,e1,e2
- D e4,e2,e3,e1
正确答案是D
选项 A:e4,e3,e2,e1 输入过程:让e1、e2、e3、e4依次从左端输入队列。输出过程:由于只能从一端输出,此时队列中元素顺序从左到右为e4 e3 e2 e1。按照先进后出原则,依次输出e4、e3、e2、e1,该输出序列可以得到。
选项 B:e4,e2,e1,e3输入过程:先让e1、e2从左端输入,e3 从右端输入 e4再从左端输入。此时队列中元素顺序从左到右为e4 e2 e1 e3。按照先进后出原则,依次输出e4,e2,e1,e3。该输出序列可以得到。
选项 C:e4,e3,e1,e2输入过程:让e1、e2从左端输入,e3、e4从右端输入。此时队列中元素顺序从左到右为e4,e3,e1,e2。按照先进后出原则,依次输出e4,e3,e1,e2。该输出序列可以得到。
选项 D:e4,e2,e3,e1输入过程:尝试各种从两端输入元素的方式。若要先输出e4,e4需最后进入队列且在队尾(输出端 )。矛盾分析:若e4在队尾,当输出e4后,接下来要输出e2,由于只能从一端输出,在e4输出后,要输出e2,则e2需在队尾,但此时若e2在队尾,e3就无法在e2之前输出,所以无法得到该输出序列。
二维数组
二维数组的特点如下:
- 数据元素数目固定。
- 数据元素具有相同的类型。
- 数据元素的下标关系具有上下界约束且下标有序。
一个m行n列的数组表示如下 
数组存储地址的计算公式
假设每个数组元素占用内存长度为len,起始地址为a,存储地址计算如下:

案例1
在一个二维数组A中,假设每个数组元素的长度为3个存储单元,行下标i为0-8,列下标j为0-9,从首地址SA开始连续存放,在这种情况下,元素A[8][5]的起始地址为( )。
- A SA+141
- B SA+144
- C SA+222
- D SA+255
正确答案:D
二维数组按行优先存储,即先存储完一行的所有元素,再存储下一行。
那么元素A[8][5]是二维数组中的第86个元素。
元素A[8][5]的起始地址 SA + 85 * 3 = SA + 255
矩阵
三对角矩阵公式如图所示

真题范例1
设有n阶三对角矩阵A,即非零元素都位于主对角线以及与主对角线平行且紧邻的两条对角线上,现对该矩阵进行按行压缩存储,若其压储空间用数组B表示,A的元素下标从0开始,B的元素下标从1开始。已知A[0,0]存储在B[1],A[n-1,n-1]存储在B[3n-2],那么非零元素A[i,j](0≤i<n,0≤j<n,|i-j|≤1)存储在B[( )]。
A 2i+j-1 B 2i+j C 2i+j+1 D 3i-j+1
正确答案:C
n阶三对角矩阵如下图所示。
在元素ai,y之前共有i行(行号从0到i-1 ),除了第一行外,其余每行都是3个元素, 因此这i行上的元素个数为(3*i-1);在行号为i时,排列在ai,y之前的元素个数为j-i+1, 合计2i+j个元素,因此元素ai,y存储在B[]中的下标为2i+j+1(因数组B是从下标1开始存放元素的)。
真题范例2
某n阶的三对角矩阵A 如下图所示,按行将元素存储在一维数组M中,设a1,1存储在M[1],那么ai,j (1<=i,j<=n且ai,j位于三条对角线中)存储在M( )。
A i+2j B 2i+j C i+2j-2 D 2i+j-2
按行存储时,aij之前有i-1行,除了第一行外,每行有3个元素,在第i行上,其之前有j-i+1个元素,因此aij之前共有(i-1)*3-1+j-i+1=2i+j-3个元素,由于ai,1存储在M[1],所以 ai,j存储在M[2i+j-3+1]。
树
树的基本概念
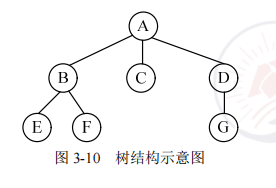
- 树的深度。一棵树的最大层数为该树的深度(或高度)。
- 结点的度。一个结点拥有子树的个数称为该结点的度。
- 叶子结点。叶子结点是指度为 0 的结点。
- 结点的层次。该结点所在树中的层次,即为该结点的层次。
- 有序/无序树。如果树中各结点的各个子树是从左到右有序排列且不能交换时,则称该树为有序树。否则称为无序树。
二叉树
二叉树与普通树的区别在于,每个节点最多只有两个孩子结点。二叉树中结点的子树分为左子树和右子树。
二叉树的性质
- 一个深度为k的二叉树最多有 2^k^-1 个结点(k>=1)。
- 在二叉树的第i层上最多有个 2^(i-1)^ 个结点(i>=1)。
- 对任何一棵二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1。即度为0的结点数比度为2的结点数多1个。
特殊的二叉树
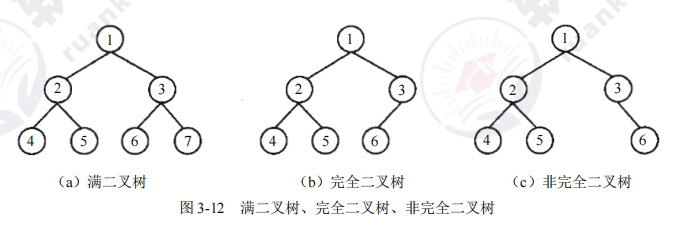
满二叉树
如果一个二叉树的层数为 K,结点总数为 2^k^ - 1 个,则它就是满二叉树,如图a所示。
完全二叉树
在一个深度为 h 的完全二叉树中,除第 h 层外(最后一层),其他各层都是满的。第 h 层所有的结点都必须从左到右依次放置,不能留空,如图 b 所示。 则这样的二叉树为完全二叉树。
平衡二叉树
平衡二叉树:树中任一结点的左右子树高度之差不超过1。
查找二叉树
查找二叉树:又称之为排序二叉树。任一结点的权值,大于其左孩子结点,小于其右孩子结点。中序遍历结果有序。
二叉树的存储结构
顺序存储
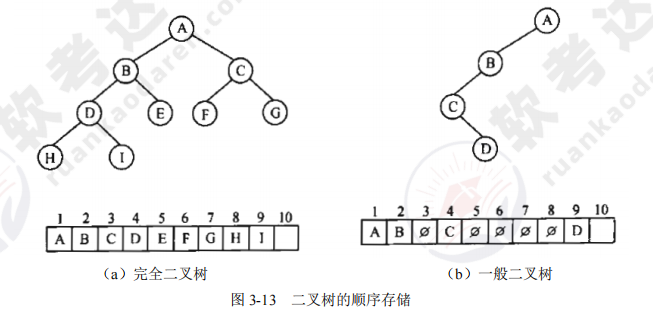
二叉树的顺序存储结构:顺序存储,就是用一组连续的存储单元存储二叉树中的节点,按照从上到下,从左到右的顺序依次存储每个节点。
在采用顺序存储时,完全二叉树与一般的二叉树相比节省了空间,这是因为一般二叉树需要添加一些“虚结点”而造成了空间的浪费,如图所示。
链式存储
二叉树的链式存储结构:一般用二叉链表来存储二叉树节点,二叉链表中除了该节点本身的数据外,还存储有左孩子结点的指针、右孩子结点的指针。每个二叉链表节点存储一个二叉树节点,头指针则指向根节点
在采用链式存储时,二叉树的链式存储可以分为二叉链表和三叉链表的存储结构,如图所示
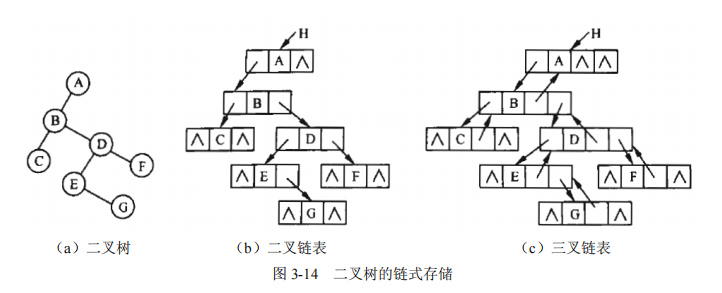
对于完全二叉树,若某个节点在数组中的存储位置为i,则其左孩子的存储位置为2i,右孩子的存储位置为2i+1。
二叉树的遍历
二叉树是一个非线性结构,而对二叉树的遍历本质上是对一个非线性结构进行线性访问的过程。通过这种遍历,可以将二叉树这种非线性结构的数据转换为线性结构的数据,从而方便存储或处理等操作。
二叉树的遍历可以分为前序、中序、后序和层次遍历四种形式。这四种遍历方式产生的结果如图所示。
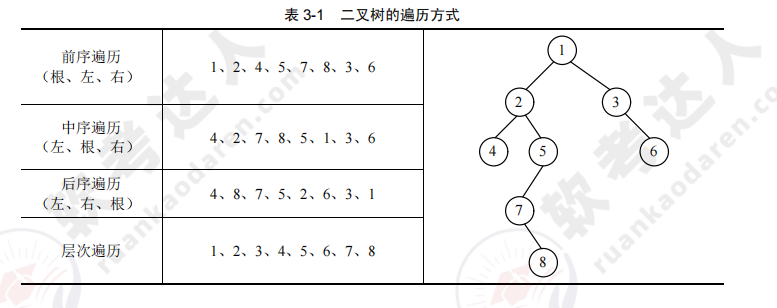
- 先序(前序)遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
- 层次遍历:按层次,从上到下,从左到右
二叉树的构造(通过遍历的序列)
单独一个序列无法确定一个二叉树。唯有根据先序遍历和中序遍历或后序遍历和中序遍历才能唯一确定一个二叉树。
必须是中序遍历搭配其他序列才能唯一确定一个二叉树。
根据先序遍历和中序遍历构造二叉树
根据先序遍历和中序遍历构造二叉树的过程如下:
- 先序遍历的第一个节点就是根节点
- 在中序遍历中找到根节点的位置,将中序遍历分为左子树和右子树
- 递归地对左子树和右子树进行构造
根据后序遍历和中序遍历构造二叉树
根据后序遍历和中序遍历构造二叉树的过程如下:
- 后序遍历的最后一个节点就是根节点
- 在中序遍历中找到根节点的位置,将中序遍历分为左子树和右子树
- 递归地对左子树和右子树进行构造
根据层序遍历和中序遍历构造二叉树
根据层序遍历和中序遍历构造二叉树的过程如下:
- 层序遍历的第一个节点就是根节点
- 在中序遍历中找到根节点的位置,将中序遍历分为左子树和右子树
- 递归地对左子树和右子树进行构造
最优二叉树(哈夫曼树)
哈夫曼树又称为最优二叉树,是一种带权路径长度最短的二叉树。
所谓树的带权路径长度,就是树中所有的叶子结点的权值乘上其到根结点的路径长度(若根结点为 0 层,叶子结点到根结点的路径长度为叶子结点的层数)。
基本概念
- 权:节点代表的值
- 路径是从树中一个结点到另一个结点之间的通路,路径上数目称为路径长度。
- 结点的路径长度:路径上的分支数目
- 结点的带权路径长度:该结点到根结点之间的路径长度乘以该节点的权值
- 树的带权路径长度:根节点到达每一个叶子节点之间的带权路径长度之和
树的带权路径长度(WPL):树中所有叶子节点的带权路径长度之和。
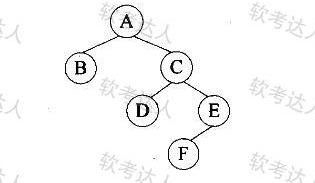
真题范例1
对下面的二叉树进行顺序存储(用数组MEM表示),已知结点A、B、C在MEM中对应元素的下标分别为1、2、3,那么结点D、E、F对应的数组元素下标为( )。
A 4、5、6 B 4、7、10 C 6、7、8 D 6、7、14
正确答案D
二叉树顺序存储规则: 对于完全二叉树,若根节点下标为i(本题中根节点A下标为1 ) ,则其左孩子节点下标为2i,右孩子节点下标为(2i + 1) 。
- 节点D:节点C下标为3,D是C的左孩子,根据规则,D的下标为 2x3=6。
- 节点E:E是C的右孩子,其下标为 2x3+1=7。
- 节点F:F是D的右孩子,D下标为6,所以F的下标为 2x6+1=14。
- 综上,节点D、E、F对应的数组元素下标为6、7、14,答案选 D。
构造最优二叉树(哈夫曼算法)
如何构造最优二叉树?构造最优二叉树的哈夫曼算法步骤如下。
- 假设有一组给定的权值集合 F,集合 F 里面包含一些权值节点。(比如{w₁, w₂, ..., wₙ})。我们需要用这些权值节点构建一个最优二叉树。
- 第一步:
- 从集合F 中选择两个权值最小的节点。将它们作为左、右子树构造一棵新的二叉树,新树的根节点的权值为这两个节点的权值之和。
- 把集合F 中删除这两个节点。并将新树根节点的权值加入到集合 F 中。
- 第二步:
- 从集合 F 剩下的节点中再次选择两个权值最小的节点,将它们作为新树的左、右子树,新树的根节点的权值为这两个节点的权值之和。
- 把集合F 中删除这两个节点。并将新树根节点的权值加入到集合 F 中。
- 重复上面步骤,直到所有节点都被合并为一棵树。
注意:
- 在构造新树的过程中,对于选出的两个权值节点,哪个作为左子树、哪个作为右子树并没有明确规定。这就导致:对于相同的一组权值,可能会构造出不同形状的最优二叉树。不过,不管形状如何变化,这些树的带权路径长度(WPL值)都是相同的,这是由权值本身决定的。
- 建议,每次选择两个权值最小的节点时,先选择权值较小的节点作为左子树,权值较大的节点作为右子树。
图
图是比树结构更复杂的一种非线性结构。
图的种类
- 无向图:图的顶点之间连接线是没有箭头的,不分方向。如图所示。
- 有向图:图的顶点之间连接线是箭头,表示从一个节点到另一个节点。如图所示。
- 无向完全图:在无向图中,若每个顶点都与其他顶点之间都有一条边相连,则称该图为无向完全图。无向完全图的n个结点的连线数为(n-1)+(n-2)+...+1 = n(n-1) / 2;
- 有向完全图:在有向图中,若每个顶点都与其他顶点之间都有两条有向边互相相连,则称该图为有向完全图。即顶点两两之间都有互通的两个箭头,则 n个节点有向完全图的的连线数为n(n-1)

图的基础概念
- 度:顶点的度是关联与该顶点的边的数目。若在有向图中,一个顶点的度为该顶点的出度和入度之和。
- 出度是以该顶点为起点的有向边的数目。
- 入度是以该顶点为终点的有向边的数目。
- 路径:存在一条通路,可以从一个顶点到达另一个顶点,有向图的路径也是有方向的。
连通图:针对无向图。若从顶点v到顶点u之间是有路径的,则说明v和u之间是连通的,若无向图中任意两个顶点之间都是连通的,则称为连通图。
连通分量:无向图G中的极大连通子图称为其连通分量。
强连通图:针对有向图。若有向图任意节个顶点间都互相存在路径即存在v到u,也存在u到v的路径,则称为强连通图。
强连通分量:有向图G中的极大连通子图称为强连通分量。
网:若图中的边带有权值,则称该图为网。
图的遍历特点
深度优先遍历
深度优先遍历:从任一顶点出发,遍历到底,直至返回。再选取任一其他节点出发,重复这个过程直至遍历完整个图。
如图所示 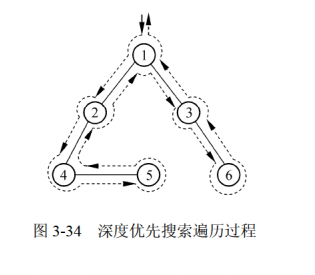
深度优先遍历的时间复杂度
- 当图使用邻接矩阵表示时,深度优先搜索遍历该图的时间复杂度为O(n^2^)
- 当图使用邻接链表来表示时,深度优先搜索遍历该图的时间复杂度为O(n+e)。其中n为节点数,e为边数。
广度优先遍历
广度优先遍历:先访问完一个顶点的所有邻接顶点,而后再依次访问其邻接顶点的所有邻接顶点,类似于层次遍历。
广度优先遍历的时间复杂度
广度优先遍历和深度优先搜索遍历图的时间复杂度相同,其不同之处仅仅在于对顶点的访问次序不同。
查找
- 顺序查找的平均查找长度为 (n+1) / 2。
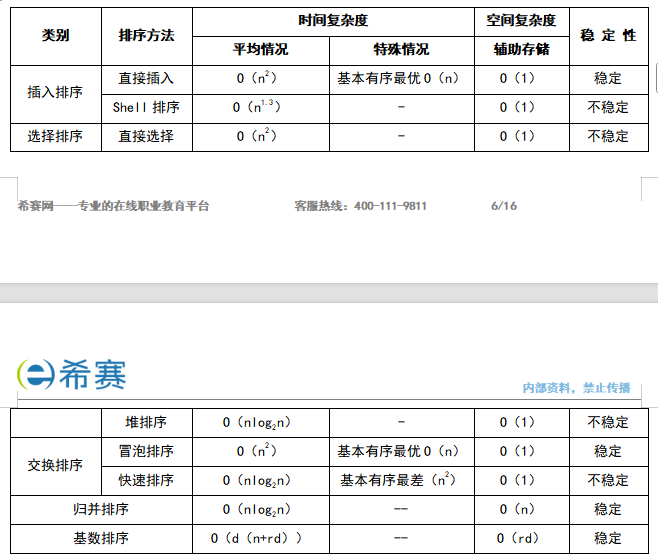
排序
稳定的排序方法:冒泡排序,直接插入排序。
常见排序方法对比如图所示